今回はワードで描いた図をブログに張り込む訓練をしようと思いました。しかし、PCだとかスマホだとか、現在の情報端末系すべて苦手、というより嫌い(大嫌い)な僕としては、新しいことをやるのも一苦労。対照的に奥さんはプログラムやネット環境をいじるのが大好き。僕は理工系の大学、大学院を出ているのに対して、奥さんは文系学部なのに!今回のブログの環境の土台作りもみんな奥さんがやってくれて、僕は出来上がった舞台の上で好き放題書いているだけ。ちなみに、僕は足し算、引き算などの四則演算は大の苦手、奥さんはそろばんやっていたので、大得意。僕はお金を使うことに意識が行く(使うために貯めるのは得意)のに対して、奥さんはお金を貯めることに意識が行く、…という本当に対照的な二人なのです。
僕は今から30年以上前に素粒子理論の大学院に入学しました。当時、僕の所属した名古屋大学の素粒子論研究室は、質量の起源についての研究が盛んでした。我々に質量があるのは、原子核や電子に質量があるからですが、原子核は陽子と中性子から成っていて、その陽子や中性子はクォーク(6種類あって、アップ、ダウン、ストレンジ、チャーム、トップ、ボトムと呼ばれて区別されている)から形成されているので、質量の起源とは、これら6種類のクォークや電子などの質量がどのように生み出されたかを研究するということなのです。ちなみに、当時はニュートリノの質量はゼロと考える傾向があったのですが、その後、質量があることが分かりました。そして、当時未発見だったトップクォークの質量を予言することに多くの研究者が興味を持っていました。
院生時代、活気ある研究室に在籍し、僕も「質量の起源について何かやれないかなあ」と期待に胸を膨らませていたと思います。それもなるべくコンピューターの助けを借りず、手計算で何か仕事が出来たらなあと思っていたのでした。ここで、理系の研究はコンピューターでガンガン数値解析をしてやるものだと思っている人が多いかもしれませんが、純粋な理学系の人々(数学や数学に近い物理の分野の人々)は、シンプルなモデルで本質をえぐり出し、手計算(と言っても半年から1年くらいはかかる計算だが)でガツンとインパクトある結果を導き出すことに価値を見出しているフシがあると思うのです。僕の指導教官もPCは苦手だったし、数学者なんかにも苦手な人は山ほどいましたからね。ある数学者はファイルのかなりの部分を削除しなければならなくなったとき、デリートキーを消しゴムで押して、その消しゴムの上に本を置いてファイルを削除し続けていました。確かに、自動で削除し続けてくれますが…。流石に現在はこのようなことはないと思いますがね。
そんな感じで僕もシンプルなモデルとか数学的な研究テーマとかをイメージして大学院生活を送ったのですが、そうそううまいモデルなんて見つけられるものではありません。結局、数値解析ガンガンの研究内容をやることになってしまいました。電子機器大嫌い、ブラインドタッチもできず、メールの送受信も一苦労、ましてや、プログラムとは何をすることなのかわからない、こんな状態の僕が数値解析になってしまったのです。当時のPCはMS DOSとか言って、すべて命令をタイプしていかないといけません。そして、ミスると「コマンド、または、フェイル名が違います」というエラー表示が現れ、これが現れると僕は震え慄いていました。そして、大学院の一年間は地獄のような苦しい研究生活となったのでした。まず、PCに慣れること、プログラムのイロハ的なことから初めて、最終的には”繰り込み群方程式”という非線形な連立微分方程式を解かなくてはいけません。プログラムはうまく走らないし、走り出したとしても途中で解が発散したりして停止してしまうという胃が痛くなるような日々でした。手計算でうまくいかないというのは、目の前に状況が見えているので気にならないのですが、PCの場合は、中がブラックボックスで一体何が上手くいかないのか見当がつかないし、電子機器嫌いがそのいやな気持を増幅してしまうのでした。1年間の苦闘の果てにかろうじて結果は出たのですが、今度はそれを修士論文にまとめなくてはいけません。その時に、数式も表示する必要があるので、Texというめんどくさいものを使って論文を書かなくてはいけないのです。このブログ(雨読編)もMathjax LatexというTexの仲間(⁉)を使って書いています。どれくらい面倒なものかというと、例えば積分
\[\int_0^x\frac{1}{\sqrt{1-x^2}}dx\]
を表示しようと思ったら、編集画面上には
\int_0^x\frac{1}{\sqrt{1-x^2}}dx
と書かなくてはいけないのです。{が抜けていたり、¥を付けるのを忘れたりすると、全く数式が表示されず、ミス探しに人生の大事な時間が奪われていくことになるのです。結局、PCなどの電子機器は不便なもので、人から時間を奪う最悪のものであるという印象を植え付けられたのでした。と、ここまで書いて、現在、僕はPCやスマホや、再びあのTexを使ってブログを書いている、それも割と夢中になっているのですから皮肉なものですね。まあ、とにかく、修士の二年間は素粒子の勉強というより、PCのプログラムとTexの勉強に費やされてしまったのでした。だからと言って、僕のPCのレベルはやっと人並みになっただけで、研究で数値解析の仕事をしている院生たちから比べると足元にも及ばないピヨピヨなレベルだったのです。それでも修論は無事に受理されて、その後、博士課程後期に在籍することになり、新たな数値解析もして学会で発表したりしたのですが、僕の中から当時とても大事だと思っていたものがなくなってしまったのでした。それは、『ぶつり』への『情熱』です。そして、いつしか『ぶつり』の『ぶ』がとれて『つり』に夢中になっていき、大学院も辞めて、黒部峡谷という大自然の中へ逃避し、そこを放浪し、黒部こそが僕の新たな大学、つまり『黒部大学』の学生になることに自分の価値を見出して行ったのでした。
ちなみに、現在の僕から見ると、当時の僕は「青いなあ」と思ってしまいますね。折角、数値解析をやるプログラムの基本を身に着けたのであれば、それをうまく使ってまとめ上げられるような小さな成果を細々とでもいいから積み上げていって、いずれは情熱も復活するだろうから、仕事と割り切って研究生活を歩んでいけばよかったのです。『情熱』とか『夢』なんていう青臭いものを前面に思い描いているのはガキみたいなもので、二十歳を越えた人間にしては幼すぎたということでしょうか。なんか、昔の研究話が長くなってしまいましたが(毎回前置きが長いですが)、この辺で本題に入りますか。
今までの変数変換(置換)は以下の図を見れば明らかだ。余計な説明はいらないかもしれないが…。
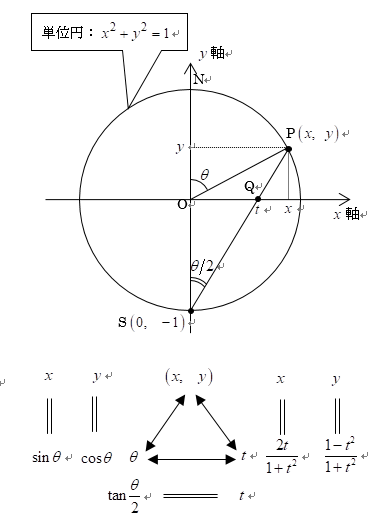
上の図を見れば、\(x=\sin\theta\)、\(x=\cos\theta\)の関係、更には\(\displaystyle t=\tan\frac{\theta}{2}\)の関係は明らかなので説明はいらないだろう。問題は、\(x\)、\(y\) と \(t\) の関係だ。以下これを導いてみよう。
まず、図のS、P(ここで、Pは単位円:\(\displaystyle x^2+y^2=1\) 上の点だ)を通る直線の方程式を求める。
SPを通る直線:\(\displaystyle y=\frac{1}{t}x-1\)
後はこの直線の式と\(\displaystyle x^2+y^2=1\) の連立方程式を解くだけだ。直線の式を
\[x=t(y+1)\]
と変形して、円の式に代入して\(y\)の二次方程式に帰着させればよい。
\[1=x^2+y^2=\lbrace t(y+1) \rbrace ^2+y^2\]
\[(y+1)\lbrace (t^2+1)y+t^2-1\rbrace=0\]
\[y=-1, y=\frac{1-t^2}{1+t^2}\]
\(y=-1\)は交点Sを表しているので、ここでは関係ない。\(\displaystyle y=\frac{1-t^2}{1+t^2}\)こそが、交点Pを表している訳である。よって、この時の\(x\)の値は
\[x=t(y+1)=t \left(\frac{1-t^2}{1+t^2}+1 \right)=\frac{2t}{1+t^2} \]
となるのだった。めでたしめでたし。
《ちょっと寄り道》円:\(\displaystyle x^2+y^2=1\)をパラメーター表示するとき、一般的には\(x=\sin\theta\)、\(x=\cos\theta\)を用いるが、時には\(t\)を用いることも出来る訳だ。この単位円の\(t\)表示が役立つ面白い例としては、ピタゴラス数を求めるという話題がある。
\(X\)、\(Y\)、\(Z\) がピタゴラス数とは、\(\displaystyle X^2+Y^2=Z^2\)を満足する整数解の組のことである。
このピタゴラス数を決定する問題は、以下のように書き換えてみると、
\[1=\left(\frac{X}{Z}\right)^2+\left(\frac{Y}{Z}\right)^2=x^2+y^2\]
但し、\(\displaystyle x=\frac{X}{Z}\)、\(\displaystyle x=\frac{Y}{Z}\)と置いた。つまり、ピタゴラス数\(X\)、\(Y\)、\(Z\)を求めることは、単位円:\(\displaystyle x^2+y^2=1\) 上の有理点 \(x\)、\(y\) を求めることに帰着されるわけだ。ここで、\(\displaystyle x=\frac{2t}{1+t^2}\)、\(\displaystyle y=\frac{1-t^2}{1+t^2}\) の関係を使う。\(x\)軸上には無数の有理点が存在し、\(t\)としてそれら無数の有理数を考えることが出来て、それらを\(\displaystyle \frac{2t}{1+t^2}\)、\(\displaystyle \frac{1-t^2}{1+t^2}\) の形にしても有理数であることに変わりわないので、単位円上の有理数の組をいくらでも求めることが出来、結果、ピタゴラス数を増産できるわけだ。具体的にやってみよう。
まず、\(\displaystyle t=\frac{1}{2}\)の時、
\(\displaystyle x=\frac{2t}{1+t^2}=\frac{4}{5}\)、\(\displaystyle y=\frac{1-t^2}{1+t^2}=\frac{3}{5}\) となるので、
\[1=\left(\frac{4}{5}\right)^2+\left(\frac{3}{5}\right)^2\]
つまり、\(\displaystyle \left(X、Y、Z\right)=\left(4、3、5\right)\)となる。
更に、\(\displaystyle t=\frac{5}{12}\)の時、
\(\displaystyle x=\frac{2t}{1+t^2}=\frac{120}{169}\)、\(\displaystyle y=\frac{1-t^2}{1+t^2}=\frac{119}{169}\) となるので、
\[1=\left(\frac{120}{169}\right)^2+\left(\frac{119}{169}\right)^2\]
つまり、\(\displaystyle \left(X、Y、Z\right)=\left(120、119、169\right)\)となる。
ちなにみ、これらのピタゴラス数は、ピタゴラスよりはるか昔の、古代バビロニア、メソポタミア文明(紀元前2300年)の時代に無数に(しかも小さい順に)求められていたというから驚きだ。人類は、古代バビロニアに栄えた文化的財産の受け渡しになんらかの理由で失敗し、その後(ピタゴラスは紀元前500年くらいだから、古代バビロニアから2000年くらい後の人)に再び発見しなければならい状況に追いやられたのだろうか。ピラミッドなどの巨石文明を支えるためには高度な数学、物理学が発展していたはずなのだから。



コメント