さきもりちゃん(我が家のDefender90)の症状は、電子制御燃料噴射システム(EFI:Electronic Fuel Injection system。メーカーごとにECU、EGIとか呼び名は色々あるらしい)が、燃料ポンプ作動時に発生する電磁波の干渉効果で信号が誤送信され、エンストしてしまうという極めてまれな症例であった。我が営業のM田さんのお客さんでこのような症状を発症した車はなかったのではないだろうか?今回のさきもりちゃんの稀な症状とは関係ないが、てんぷらさんとの間で話題になった”ノックセンサー”と”ノッキング”について勉強も兼ねてまとめておきたい。
追伸 その後、三回目のエンストが発生したのである。そのため、燃料ポンプ作動時の電磁波の干渉効果ではないことが明確になった。ということは、ここで取り上げたノッキングセンサー関連のエンストとも考えられるのである。今のところ原因は究明できていないが、もしかしたら、てんぷらさんの指摘通りなのかもしれない。
今回のエンジンストールとチェックセンサー点灯の件で、ノックセンサーが原因で似たような事例が発生しているという情報がてんぷらさんからもたらされたのだ。このノックセンサーのノックとは、エンジンのノッキングのこと。それじゃあ、ノッキングとは何か?ということになる。
ノッキングをしっかり理解するためには、ガソリンエンジンのメカニズムを理解しておかなくてはいけない。そこで、ガソリンエンジン(以下エンジンと略す)について学んだことをまとめておこう。まず、自動車のエンジンはガソリンの燃焼ガスから動力(外に仕事)を取り出すために、「吸気」、「圧縮」、「燃焼」、「排気」の4つの行程を行っている。つまり、エンジン内のシリンダーにガソリンが混ざった空気(混合気)を注入し、それをピストンで圧縮し、スパークプラグで点火し燃焼させて圧力の増した混合気がピストンを押し下げ、ピストンの上下動を作りだし、それを回転エネルギー に転換して車を動かしているのである。ピストンの片道の運動をストロークといい、ピストンの上(圧縮)・下(膨張)・上(圧縮)・下(膨張)で1セット(1サイクル)となるエンジンが以下の4ストローク(フォースト)エンジンだ。
①吸気
ピストンが降下(膨張)を始めたとき、吸気バルブが開き、混合気がシリンダー内に流れ込む。
②圧縮
吸気バルブおよび排気バルブは閉じられていて、混合気に充たされたシリンダーをピストンが上昇し、断熱的に圧縮する。この時、混合気の温度も上昇する。
③燃焼
ピストンが一番上に来た時(シリンダーの体積が最小!これを上死点[TDC:Top Dead Center]と言うらしい)、スパークプラグで点火し、ガソリンを燃焼させる。燃焼によってピストンを下向きに押す圧力が増大。ピストンは降下を開始。
④排気
最下点(シリンダーの体積最大!これを下死点[BDC:Bottom Dead Center]という)に押し下げられたピストンは慣性のため再び上昇に転じる。この時、排気弁が開き、燃焼済みのガス(排気ガス)を外へ排出する。ピストンが上死点に達し、排気弁が閉まり、ピストンの降下に伴い吸気弁から新たな混合気がシリンダー内に導き入れられてきて、最初の状態に戻る。以下これを繰り返していく。
ここで、エンジンの燃焼の時の温度は2000℃であり、鉄でさえも溶けてしまう。一方、ピストンは主にアルミでできており、アルミの融点は660℃である。であるなら、常識的にはピストンはどろどろになってしまうはずなのに、何故に溶けないのか。それは空気の被膜層(数十ミクロン)がピストンやシリンダーを覆っているからなのだ。例えていうなら、サウナで水風呂に入った時、最初の冷たさを我慢して浸かっていると、しばらくするとあまり冷たく感じなくなる。それは、皮膚と水との間に空気の被膜層が出来て、直接冷たい水が肌に触れるのを防いでいるからだ。そこに、他のおっさんがジャブンと水風呂に入ってくると、水がかき乱され被膜層が壊れてしまうため、「ヒィーッ!冷たい」ということになってしまう。これと同じことがエンジンのシリンダー内でも起こっていて、おっさんがジャブンと水風呂に入ってくることがノッキングに対応している!?。通常、ピストンが上死点に来た時にスパークプラグの着火で燃焼が起こり、その火炎が広がっていき、ピストンを押し下げる圧力を作り出しているわけだ。一般に、気体(混合気)を圧縮すると温度が上昇する。これは、自転車に空気入れで空気を入れる時、ピストンで圧縮した圧縮空気を注入していくわけだが、入れ終わった後の空気入れのシリンダーを触るととても熱くなっている(詳しくは後で述べるポアソンの関係式だ)ことから想像できる。つまり、③の燃焼過程で、火炎が広がるとき、隅っこに追いやられた燃え残りの混合気が断熱的圧縮を受けて温度上昇し自然発火を起こし、爆発して圧力波が発生!反対側のシリンダー隔壁に圧力波が衝突(反射)する時に、カンカンとかキンキンとかの甲高い音を発生するのがノッキングという現象だ。この圧力波はピストンやシリンダーの間の空気の被膜層を破壊し、シリンダーやピストンの温度は上昇してしまう。すると、今度は②の圧縮過程の段階で高温となった混合気が自然着火を起こして爆発。これにより被膜層壊れピストンのさらなる温度上昇を誘発し、以下、自然着火がどんどん加速しそのうちエンジンが壊れてしまう。このように、ノッキングとはエンジンにとって極めて切実な現象なのだ。しかし、エンジンの効率(熱効率)やエンジンのパワーを上げようとすると、ノッキングの危険性が高まり、これらは両立しないのである。人類のエンジン開発の歴史は、ノッキングをいかに避けるかの技術の開発の歴史と言っても過言ではない(ように防人には思えてしまう)。このようにエンジンにとって切実なノッキングが発生すると、エンジンに特異な振動が発生するので、この振動を検知し、ノッキングの発生をいち早くEFIに知らせるのがノックセンサーの役目なのである。気圧や湿度、吸気温度の違い、エンジンの個体差などによりノッキングが起こる状況もバラバラなので、ノックセンサーを使ってギリギリのところで監視体制を整えているといったとこか。そして、ノックセンサーから信号が送られてくると、EFIは空気と燃料(ガソリン)との混合比を変えたり、スパークプラグの点火のタイミングを調整してエンジンを正常な燃焼に戻すのだが、このノックセンサーに異常があると、エンジン警告灯を点灯させたり、エンジンストールの原因になったりしてしまうのだろう。ノックセンサーの改良型が登場するようなので、もしノッキングがらみの不調があったらランドローバーのディラーに聞いてみた方が良いのかもしれない。
以下ではもう少し定量的に見てみよう。上記の①、②、③、④の過程を\(p-V\)図に描いてみると以下のようになる。これはオットーサイクルと呼ばれ、ガソリンエンジンの理論的基盤をなすものである。ちなみに、オットーとはドイツの発明家Nikolaus August Ottoのことである。
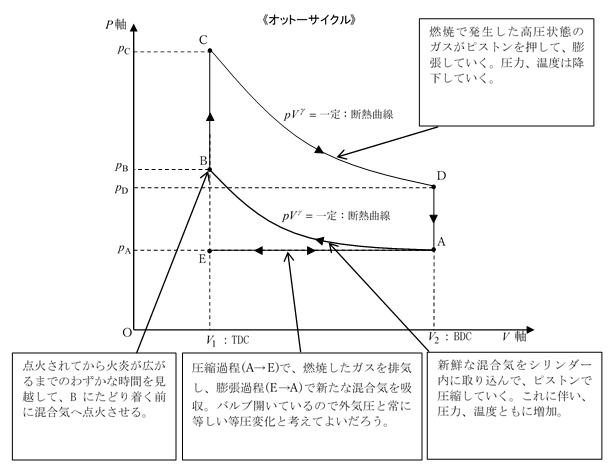
上図のようにフォーストエンジンのサイクルはA→B→C→D→A→E→Aで1サイクルとなる。ここで、\(V_2-V_1\)を排気量と呼ぶ。例えば、我がさきもりちゃん(ディフェンダー90)のガソリンエンジンは4気筒の排気量2リッターのエンジンなので、2リッターを4で割ると、\(V_2-V_1=0.5\)リッターとなる。
A→B:断熱圧縮過程…(ポアソンの関係式:\(pV^{\gamma}=p_{A}V_{2}^{\gamma}=p_{B}V_{1}^{\gamma}=一定\))
B→C:スパークプラグで点火されガソリンの燃焼熱が加わり、定積的に圧力が上昇
C→D:断熱膨張過程…(ポアソンの関係式:\(pV^{\gamma}=p_{C}V_{1}^{\gamma}=p_{D}V_{2}^{\gamma}=一定\))
D→A:熱を捨てて、圧力を下げ状態Aに戻す。
A→E:ピストンは慣性で再び上昇に転じ、それと共に排気弁を開き、シリンダー内の排気をする。
E→A:排気弁を閉じ、吸気弁を開いて、新鮮な混合気をシリンダー内に取り入れる。
ここで、\(\gamma\)は比熱比で、定積モル比熱\(C_V\)、定圧モル比熱\(C_P\)、それとマイヤーの関係式” \(C_P=C_V+R \) “を用いて、
\[\gamma=\frac{C_P}{C_V}=\frac{C_V+R}{C_V}>1\]
と定義されていることに注意しておこう。
以下ではこのオットーサイクルの熱効率\(e\)を計算してみよう。そのために、以下のことを確認しておく必要がある。まずは、
\[熱力学の第一法則:dQ=dU+dW\]
である。ここで各項を説明しておく。
\(dQ\):気体(混合気)に加えた熱量
B→Cではガソリンの燃焼熱が加えられ、D→Aでは気体の熱を奪い圧力を下げる。
\(dU\):気体(混合気)の内部エネルギーの変化
内部エネルギーとは気体自体が持つエネルギー(運動エネルギーや相互作用エネルギー)の総合計のこと。理想気体(分子同士の衝突や反応を無視した気体)の場合は簡単に計算出来て、\(U=\frac{f}{2}nRT\)となる。ここで、\(f\)は分子の自由度で、単原子分子のとき\(f=3\)、二原子分子のとき\(f=5\)、二原子分子が高温になると振動の効果が入ってきて\(f=7\)となる。この\(f\)は気体の種類や状態ごとで値は変わるものだ。この内部エネルギーは定積モル比熱を用いて\(U=nC_{V}T\)とも書ける。
\(dW\):気体(混合気)が外へした仕事
\(dW=Fdx=PSdx=PdV\)となる。この式より、気体がする仕事は\(p-V\)図上で、\(V\)軸とグラフで囲まれる面積であることがわかる。ここで、膨張の時は\(dV>0\)で正の仕事、圧縮の時は\(dV<0\)で負の仕事となる。
次に、気体は理想気体であると仮定して、
\[状態方程式:pV=nRT\]
を認めるものとする。さて、楽しい計算をしてみよう。
A→Bについて!
\(\displaystyle内部エネルギーの変化:U_{AB}=\int_{A}^{B}dU=\frac{f}{2}nR\int_{T_{A}}^{T_{B}}dT\)
\(=\displaystyle \frac{f}{2}nR(T_{B}-T_{A})=\frac{f}{2}(p_{B}V_{1}-p_{A}V_{2}) \)
\(\displaystyle気体が外へした仕事:W_{AB}=\int_{A}^{B}dW=\int_{V_2}^{V_1}pdV\)
と求めることもできるが、断熱変化の時は熱力学の第一法則を用いてやるのが簡単だ。
\(\displaystyle 0=U_{AB}+W_{AB} より W_{AB}=-U_{AB}=-\frac{f}{2}(p_{B}V_{1}-p_{A}V_{2}) \)
B→Cについて‼
定積変化なので気体は仕事をしない。そのため、気体に加えた熱量\(Q_{AB}\)は熱力学の第一法則から求める(or定積モル比熱の定義式から求めてもよいが)
\(\displaystyle Q_{BC}=U_{BC}+0=\frac{f}{2}nR(T_C-T_B)=\frac{f}{2}(p_{C}V_{1}-p_{B}V_{1}) \)
同様に、C→D、D→Aもやればよい。また、A→EとE→Aは仕事は相殺し合うし、気体を排気、吸入するだけなので、熱効率の計算には効いてこないので考えなくてよい。よって、以下の表を得る。

以上より熱効率\(e\)を求めてみよう。熱効率とは気体(熱機関、つまり、エンジン)に投入した熱量(ガソリンの燃焼熱)\(Q\)に対する、外にした仕事\(W\)の比率である。早速、オットーサイクルの場合に計算してみよう。この計算の途中でポアソンの関係式の結果、
\[p_{A}=p_{B}\left(\frac{V_{1}}{V_{2}}\right)^{\gamma}, p_{D}=p_{C}\left(\frac{V_{1}}{V_{2}}\right)^{\gamma} \]
を代入するので注意してもらいたい。
\(\displaystyle e=\frac{W}{Q}=\frac{W_{AB}+W_{BC}+W_{CD}+W_{DC}}{Q_{BC}}\)
\(\displaystyle =-\frac{p_{B}V_{1}-p_{A}V_{2}+p_{D}V_{2}-p_{C}V_{1}}{p_{C}V_{1}-p_{B}V_{1}}\)
\(\displaystyle =\frac{p_{C}V_{1} \left(1-\left(\frac{V_{1}}{V_{2}}\right)^{\gamma-1}\right)-p_{B}V_{1} \left(1-\left(\frac{V_{1}}{V_{2}}\right)^{\gamma-1}\right)}{\left(p_{C}-p_{B}\right)V_{1}}\)
\(\displaystyle =1-\left(\frac{V_{1}}{V_{2}}\right)^{\gamma-1}\)
ここで、圧縮比\(\kappa=\frac{V_2}{V_1}\)を導入すると、上記の熱効率は
\[e=1-\kappa^{1-\gamma}\]
とも書ける。ここで、\(\kappa>1\)、\(1-\gamma <0 \)であることを思い出しておくと、熱効率\(e\)を上げるためには(燃費を上げるためには)、圧縮比\(\kappa\)をなるべく大きくしたい(自然吸気の場合の圧縮比は15くらいまで行っているようだが,過給機による吸気だと圧縮比は10前後)。また、エンジンパワーを大きくするためには空気をなるべく多く取り込んで燃焼を促進したい。つまり過給機(エンジンの回転でファンを回して空気を取り込むスーパーチャージャーや排気ガスを利用してファンを回転させるターボチャージャーがある)で空気を取り込むのだが、するとシリンダーの圧が上昇するのでピストンの圧縮による温度上昇も甚だしい。どちらにせよ、ピストンの圧縮に伴う混合気の温度上昇は大きくなる。すると、自然着火しやすくなるので、ノッキングの恐れが生じてしまうのである。そこで、ガソリンのオクタン価を上げ(ハイオクを使う)て燃えにくくする(耐ノック性が比較的高いイソオクタン(2,2,4-トリメチルペンタン)の比率を大きくする)とか、ガソリンを直接シリンダーに噴射(Gasoline Direct Injection)して、それが気化するときに気化熱を周囲から奪うので、その効果で温度上昇を防いでノッキングを起こしにくくするとか、様々な工夫がなされているようだ。
最後に、断熱膨張圧縮の時のポアソンの関係式を導出しておこう。まず、断熱過程なので、
\[熱力学の第一法則:0=dU+dW=nC_V dT+pdV\]
となる。この式より、気体が膨張の時、つまり、\(dV>0\)の時は\(dT<0\)となり温度降下。一方、\(dV<0\)の圧縮の時は\(dT>0\)となり温度上昇となることがわかる。
さて、状態方程式の微分とマイヤーの関係式より、
\[Vdp+pdV=nRdT=n\left(C_P-C_V\right)dT\]
となる。この式に第一法則を\(dT\)について解いたものを代入して、比熱比\(\gamma=\frac{C_P}{C_V}\)を用いると、
\[Vdp+pdV=nRdT=-\left(\gamma-1\right)pdV\]
\[\frac{1}{p}dp=-\gamma \frac{1}{V}dV\]
となる。この両辺を積分すると、\(C\)を積分定数として、
\[C=\ln p+\gamma\ln V=\ln p+\ln V^{\gamma}=\ln\left(pV^{\gamma}\right)\]
となる。\(\ln\)が一定の\(C\)ということはその中が一定なので、ポアソンの関係式
\[pV^{\gamma}=一定\]
が示せた。

中さんのレンジローバーSEの納車式の時、さきもりちゃんのお見舞いもしたのだが。彼女は遥か奥に駐車されていた。彼女を駐車場から出そうとするなら、何台もの車を移動させなくてはいけないだろうと思われた。これを見たとき、さきもりちゃんの退院はまだ当分先だと思われた。エンジンストールの原因は本当に確定しているのだろうか?このようなことが繰り返されて行って、保証期間が過ぎてしまったらどうなるのだろうか?いろいろと不安が頭をよぎったりしたのだった。



コメント